

MedFriendly®


Upper Motor Neuron
Upper motor neurons (often abbreviated as UMNs) are
neurons (nerve cells) in the motor cortex (an area in the
front part of the brain that helps control motor
functioning) that compose two types of nerve tracts
(paths). The first are the corticospinal tracts, which are
nerve paths connecting the cortex (outermost part of
the brain) and the spinal cord. The second are the
corticobulbar tracts, which are nerve paths from the top
part of brain to the lower part of the brain called the
brain stem.
FEATURED BOOK: Principles of Neurology by Adams and Victor
The brain stem area is referred to as bulbar because is has a bulb-shaped appearance.
The brainstem connects the brain with the spinal cord and controls many functions crucial
for life to continue such as breathing. Lower motor neurons send messages via the upper
motor neurons to the skeletal muscles (e.g., muscles in the arms and legs).
The term "upper motor neuron" is actually misleading because upper motor neurons are
not really motor neurons. They are called motor neurons because when they are
stimulated they produce movement and when they are destroyed, severe movement
disorders result. As an example, in upper motor neuron paralysis, paralysis (loss of
movement and/or sensation) is caused by damage to the cell bodies and/or axons (parts
of nerve cells that send messages) of the upper motor neurons.
"Where Medical Information is Easy to Understand"™
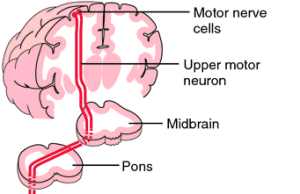
The upper motor neuron.














